Ćwiczenie 2.

 

Podstawy modelowania i symulacji

 

1.        RÓWNANIE RÓŻNICZKOWE

 

Większość obiektów dynamicznych da się opisać równaniem różniczkowym postaci:

 

a_ny⁽ⁿ⁾+a_n-1y^(n-1)+... +a₁y¹+a₀y=u(t)

 

 

 

 

Każde równanie różniczkowe n-tego rzędu da się sprowadzić do układu n równań rzędu 1-go. Zróbmy następujące podstawienia:

y(t)=x₁(t)

x’₁=x₂

x’₂=x₃

:

x’_n-1=x_n

wówczas:

Otrzymamy układ równań 1-go rzędu następującej postaci:

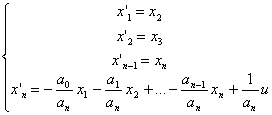
który w notacji macierzowjma następującą postać:

=

 

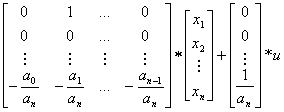
Takie równanie macierzowe zapiszemy teraz w postaci funkcji Matlaba:

 

row_rozn.m

 

function dx=row_rozn(t,x)

global  A B

dx=A*x+wymuszenie(t);

 

Funkcja reprezentująca wymuszenie (wektor sygnałów wejściowych będzie miała następującą postać:

 

wymuszenie.m

 

function u=wymuszenie(t)

if t >= 0

u = 1

else

u = 0

end

 

Aby numerycznie rozwiązać powyższe równanie różniczkowe w Matlabie (tzn. otrzymać wartości funkcji y dla odpowiadających im wartości chwil czasowych t należy użyć funkcji ode23 lub ode45. Skrypt rozwiązujący takie równanie powinien mieć następującą postać:

global A B

A=[  ]

B=[  ]

[t,y] = ode23(‘rów_różn’,[t₀ t_k],y₀)

gdzie:  t,y – rozwiązania, wektory odpowiednio chwil czasowych i wartości funkcji,

            ‘rów_różn’ – nazwa funkcji definiującej rozwiązywane równanie różniczkowe,

            t₀, t_k – przedział czasu, w którym ma być rozwiązywane równanie różniczkowe,

            y₀ – warunki początkowe (wartość zmiennych x₁ …x_n w chwili t₀.

 

Przykład:

Oscylator liniowy z tłumieniem (obciążnik na sprężynie)

   (przyjęto, iż nie występuje wymuszenie u=0)

 

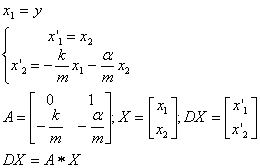
Funkcja reprezentująca powyższy układ równań różniczkowych:

oscylator.m

 

function DX=oscylator(t,X)

global A

DX=A*X;

 

Skrypt rozwiązujący takie równanie:

 

global A ;

k=1;

m=1;

a=0.5;

A=[0 1 ; -k/m -a/m];

y0=[5 0];   (warunek początkowy dla położenia różny od 0, x₁=5)

[t,y]=ode23('oscylator',[0 20], y0);

plot(t,y(:,1));

 

2.  WIZUALIZACJA SYMULOWANYCH PROCESÓW

 

Możliwości wizualizacji procesów symulowanych w Matlabie zostaną pokazane na przykładzie modelu sprężyny z obciążeniem. Wizualizowany obiekt przedstawiony został na poniższym rysunku

 

 

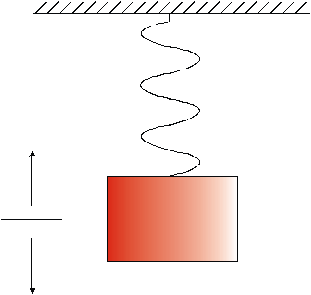
Rys. Wizualizowany model

 

Załóżmy, że mamy (otrzymane z eksperymenu symulacyjnego) dwa wektory: t reprezentujący kolejne chwile czasowe symulacji i wektor y odpowiadających tym chwilom wartości położenia środka obciążnika.

Najpierw należy odpowiednio przeskalować okno, w którym ma być przeprowadzana nasza wizualizacja:

y_max= 20;

y_min= -20;       % zakres na osi Y w którym może przemieszczać się obciążnik

x_max= 10;

x_min= -10;       % zakres na osi Y

axis([x_min  x_max  y_min  y_max];

Następnie zostaną określone początkowe współrzędne kolejnych wierzchołków obciążnika (prostokąta) dla osi X:

x_p=[ -2  -2  2  2];

i dla osi Y:

y_p=[ y(1)-1  y(1)+1  y(1)-1  y(1)+1];

Kolejnym etapem jest pierwsze narysowanie obciążnika (dodatkowo zmiennej idp zostanie przypisany identyfikator narysowanego prostokąta (obiektu patch):

idp=patch(x_p, y_p, ‘r’, ‘erasemode’,’xor’)

Ostatnim etapem jest stworzenie pętli wyświetlającej nasz prostokąt w kolejnych punktach (zmiana współrzędnych wektora y_p):

for i=1:length(t),

  y_p=[ y(i)-1  y(i)+1  y(i)-1  y(i)+1];

  set(idp,’xdata’, x_p, ‘ydata’, y_p);    % zmiana współrzędnych w obiekcie o identyfikatorze idp

  drawnow;                                     % wyrysowanie prostokąta w nowym położeniu

  pause(0.05)

end

 

Aby być w pełni usatysfakcjonowanym należy naszą wizualizację uzupełnić o sprężynę:

y_max= 20;

y_min= -20;

x_max= 10;

x_min= -10;

axis([x_min  x_max  y_min  y_max];

x_p=[ -2  -2  2  2];

y_p=[ y(1)-1  y(1)+1  y(1)-1  y(1)+1];

v=0:0.1:6*pi;                                     

x_s=sin(v)% współrzędne sinusa po zmiennej X

y_s=(y_max-y_p(2))/(6*pi)*v+y_p(2);             % współrzędne sinusa po zmiennej Y

idp=patch(x_p, y_p, ‘r’, ‘erasemode’,’xor’)

idl=line(x_s, y_s, ‘erasemode’,’xor’)    %pierwsze narysowanie lini w kształcie sprężyny

for i=1:length(t),

  y_p=[ y(i)-1  y(i)+1  y(i)-1  y(i)+1];

  set(idp,’xdata’, x_p, ‘ydata’, y_p);

  set(idl,’xdata’, x_s, ‘ydata’, y_s);

  drawnow;

  pause(0.05)

end