Ćwiczenie 3.
Postacie
modeli układów dynamicznych w Matlabie
1.
OPIS W
PRZESTRZENI STANU
Cechą charakterystyczną fizycznych układów dynamicznych jest zdolność do akumulowania energii. Oznacza to, że jeżeli na układ dynamiczny działa sygnał wejściowy u(t), to znajomość tego sygnału w chwili t=t0 nie wystarcza do określenia sygnału wyjściowego y(t0). Na wartość tego sygnału w chwili t0 wpływa bowiem również przebieg sygnału u(t) w przeszłości, dla t< t0, decydujący o nagromadzonej w układzie energii. Aby odciąć się od przeszłości, wprowadza się pojęcie stanu. Stan jest to minimalna liczba danych charakteryzująca przeszłość układu dynamicznego i umożliwiająca jednocześnie określenie jego zachowania się w przyszłości (pod warunkiem znajomości przyszłych sygnałów wejściowych). Dla przykładu załóżmy, że modelem matematycznym układu dynamicznego jest równanie różniczkowe zwyczajne rzędu n-tego
![]()
Znajomość prawej strony równania modelującej sygnał wejściowy u(t), oraz warunków początkowych y(t0),...,y(n-1(t0) w liczbie równej rzędowi równania, określa jednocześnie rozwiązanie, czyli znajomość sygnału wyjściowy układu y(t). Można więc stwierdzić, że warunki początkowe określają stan układu w chwili t0.
Każde równanie różniczkowe rzędu n-tego
można sprowadzić do postaci normalnej, czyli przedstawić w postaci
układu n równań różniczkowych rzędu pierwszego 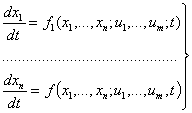
przy czym xi=xi(t),
ui=ui(t).
Znajomość
zmiennych xi(i=1,2,...n) w chwili t0 oraz
sygnałów ui(t)(i=1,2,...,m) dla t≥ t0
umożliwia określenie zachowania się układu dla wszystkich chwil t≥ t0.
Zmienne xi określają więc w każdej chwili stan układu i stąd
są nazwane współrzędnymi stanu.
Zapis równań można uczynić bardziej przejrzystym stosując symbolikę
wektorową ![]()
przy czym: x=(x1, x2,...,xn)T ; u=(u1, u2,...,um)T; f=(f1, f2,...,fn)T;
n-wymiar wektora stanu
m- wymiar wektora sygnałów
sterujących.
Wektor x, którego elementami są współrzędne stanu, nazywa się wektorem
stanu, a przestrzeń n-wymiarową o współrzędnych xi(i=1,2,...,n)
nosi nazwę przestrzeni stanu, a
powyższe równanie nosi nazwę równanie stanu. Zmiany wektora stanu
z biegiem czasu tworzą w przestrzeni stanu krzywą nazwaną trajektorią stanu.
Sygnały y=y(t), które zjawiają się na wyjściu układu, są pewnymi
funkcjami współrzędnych stanu, mogą być również zależne bezpośrednio (nie przez
współrzędne stanu) od sygnałów wejściowych u. Równanie
y=fy(x,u)
nazywa się równaniem wyjścia układu dynamicznego. Zauważmy, że są to
równania algebraiczne, bowiem cały opis dynamiki układu jest zawarty w równaniu
stanu .
W ten sposób pełny opis układu obejmuje równania stanu i wyjścia, co w
notacji macierzowej ma następującą postać:.
![]()
![]()
Równaniom tym odpowiada schemat:
Rys. Schemat liniowego układu dynamicznego
opisanego w przestrzeni stanu (ang. state space
- ss)
A - macierz układu
B - macierz wejścia
C - macierz wyjścia
D - macierz tranzycyjna (bezpośredniego sterowania)
Przykład:
Weźmy pod uwagę oscylator
liniowy z tłumieniem (obciążnik na sprężynie) opisany następującym równaniem
różniczkowym:
![]()
![]()
Przyjmując następujące współrzędne
stanu:
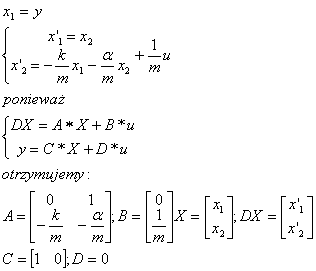
Załóżmy, że zależność pomiędzy sygnałem wejściowym i wyjściowym można opisać
liniowym równaniem różniczkowym rzędu n
![]()
Zamiast bezpośredniego, analitycznego rozwiązywania tego równania,
rozwiązanie można osiągnąć na drodze przekształceń algebraicznych
przetransformowanego układu równań. Stosuje się do tego celu transformację
Laplace'a
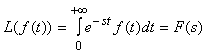
Otrzymuje się transmitancje, które wyrażają stosunek sygnału wyjściowego Y(s)
do wejściowego X(s) ,przy
zerowych warunkach początkowych:
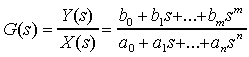 przy czym: n ≥ m
przy czym: n ≥ m
Przykład:
Weźmy pod uwagę oscylator
liniowy z tłumieniem (obciążnik na sprężynie) opisany następującym równaniem
różniczkowym:
![]()
Poddając obie strony r-nia transformacie Laplace’a otrzymujemy:
m s2 Y(s) + α s Y(s) + k Y(s) = U(s)
![]()
Powyższa
postać transmitancji nosi nazwę transmitancji
wielomianowej (ang.
transfer function - tf) ![]()
W Matlabie
model takiej transmitancji wprowadza się podając wektory współczynników licznika
![]() (ang.
numerator):
(ang.
numerator):
L = [bm bm-1 … b0]
oraz mianownika (ang. denominator)
M = [an an-1 … a0]
w malejącej potędze potędze s.
Transmitancję można również przedstawić w postaci zero-biegunowa (ang. zero pole - zp)
![]()
gdzie: z1 ... zn - zera transmitancji, [z1,z2,...,zm]=roots(L) ,
p1 ... pn - bieguny (ang. poles) transmitancji, [p1,p2,...,pn]=roots(M),
k - współczynnik wzmocnienia
Możliwa jest konwersja jednej postaci w drugą. Służą do tego polecenia:
[z,p,k]=tf2zp(l,m) -
zmienia postać wielomianową na zero-biegunową transmitancji
[l,m]=zp2tf(z,p,k) -
zmienia postać zero-biegunową na wielomianową transmitancji
[l,m]=ss2tf(A,B,C,D) – zmienia opis w przestrzeni stanu na
transmitancję
[A2,B2,C2,D2]=tf2ss(l,m) - zmienia transmitancję na opis w przestrzeni
stanu
Przykład:
Jeżeli ![]() , to
, to
» l=[2 4] <Enter>
» m = [3 0
4 5] <Enter>
Ekran MATLABA powinien
wyglądać tak:
|
» l=[2 4] l = 2 4 » m = [3 0 4 5]
m = 3 0
4 5 |
W przestrzeni roboczej MATLABA istnieją teraz zmienne l (licznik transmitancji) i m (mianownik).
Wprowadź polecenie printsys(l,m) , otrzymasz
|
num/den =
2 s + 4
------------------ 3 s^3 + 4 s + 5 |
W Matlabie istnieje również możliwość generacji
standardowych modeli obiektów dynamicznych:
-
obiekt oscylacyjny
- ord2
-
opóźnienie transportowe: pade(T0,n) ,
gdzie: n - jest rzędem
wielomianu, którym jest to opóźnienie przybliżone.
[l,m]=pade(T0,n)
[A,B,C,D]=pade(T0,n)
- model generowany losowo : rmodel(n) ; gdzie: n - jest to rząd transmitancji.
3.
SYMULACJA Z
UŻYCIEM FUNKCJI CONTROL TOOLBOX
Charakterystyki czasowe:
·
Skokowa - polecenie step
step(l,m)
lub step(A,B,C,D)
·
Impulsowa - polecenie impulse
impulse(l,m)
lub impulse(A,B,C,D)
·
Dowolna
- polecenie lsim
y=lsim(l,m,u,t)
y=lsim(A,B,C,D,u,t,x0)
gdzie: u(t) – wektor wartości sygnału
wejściowego dla kolejnych chwil t
x0 – wektor wartości początkowe
Charakterystyki częstotliwościowe:
·
Bode’go - polecenie bode
bode(l,m)
· Nyquist’a - polecenie nyquist
nyquist(l,m)