SYMULACJA UKŁADÓW DYNAMICZNYCH

 

---

Kulka i belka

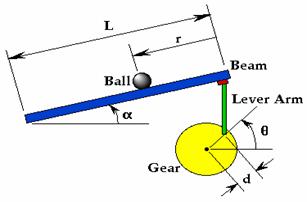
Metalowa kulka stacza się po pochyłej belce. Belką tą można poruszać, zmieniając jej kąt nachylenia względem poziomu w sposób pokazany na rysunku.

 

 

Dane:

M - masa kulki -                  0.11 kg  

d - promień zaczepu dzwigni 0.03 m

R - promień kulki                               0.015 m

g - przyspieszenie ziemskie -9.8 m/s^2

L - długość belki                 1.0 m.                    

J - moment bezwł. kulki -                9.99e-6 kgm^2

r - chwilowe położenie kulki

 

Zadaniem naszym jest stabilizacja położenia kulki w obecności losowych zakłóceń ( Regulator PID lub sprzężenie od stanu z przemieszczeniem biegunów).

 

MODEL MATEMATYCZNY:

Równanie ruchu kulki, po linearyzacji wokół alfa=0 .Równanie wiążące kąt odchylenia belki z kątem obrotu wału silnika można aproksymować liniową zależnością .

Wynika stąd równanie, z którego otrzymamy transmitancję oraz zmienne stanu .

 

W ćwiczeniu należy:

·       zbudować model matematyczny (ss i tf), przeprowadzić symulację sytuacji, w której następuje wytracenie kulki z położenia równowagi (popchniecie kulki, zmiana kąta nachyleni belki). Co stanie się z kulką?

·       „dobudować” do układu regulator PID lub PI lub PD, dobrać jego nastawy tak, aby zapewnić maksymalnie krotki czas ustalania pozycji kulki.

·       wykonać powyższy podpunkt dla układu dyskretnego

 

 

Dla chętnych / chcących dostać lepszą ocenę

·       Zaproponować realizację sprzętowo-programową układu.

·       wyprowadzić model matematyczny układu, w którym zaczep dźwigni silnika znajduje się w dowolnym miejscu belki (np. w połowie jej długości, 75%)